Table of Contents
Get source code for this RMarkdown script here. Download the cheatsheet here.
This tutorial is also available on Medium, Towards Data Science.
Consider being a patron and supporting my work?
Donate and become a patron: If you find value in what I do and have learned something from my site, please consider becoming a patron. It takes me many hours to research, learn, and put together tutorials. Your support really matters.
How does the numpy reshape() method reshape arrays? Have you struggled understanding how it works or have you ever been confused? This tutorial will walk you through reshaping in numpy.
Use reticulate R package to run Python in R
library(reticulate)
use_condaenv(condaenv = "python376", conda = "/opt/anaconda3/bin/conda") # python environmentCreate a Python numpy array
Use np.arange() to generate a numpy array containing a sequence of numbers from 1 to 12. See documentation here.
import numpy as np
a1 = np.arange(1, 13) # numbers 1 to 12
print(a1.shape)(12,)
print(a1)[ 1 2 3 4 5 6 7 8 9 10 11 12]

Reshape with reshape() method
Use reshape() method to reshape our a1 array to a 3 by 4 dimensional array. Let’s use 3_4 to refer to it dimensions: 3 is the 0th dimension (axis) and 4 is the 1st dimension (axis) (note that Python indexing begins at 0). See documentation here.
a1_2d = a1.reshape(3, 4) # 3_4
print(a1_2d.shape)(3, 4)
print(a1_2d)[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
If you want numpy to automatically determine what size/length a particular dimension should be, specify the dimension as -1 for that dimension.
a1.reshape(3, 4)
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
a1.reshape(-1, 4) # same as above: a1.reshape(3, 4)
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
a1.reshape(3, 4)
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
a1.reshape(3, -1) # same as above: a1.reshape(3, 4)
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
a1.reshape(2, 6)
array([[ 1, 2, 3, 4, 5, 6],
[ 7, 8, 9, 10, 11, 12]])
a1.reshape(2, -1) # same as above: a1.reshape(2, 6)
array([[ 1, 2, 3, 4, 5, 6],
[ 7, 8, 9, 10, 11, 12]])
Reshape along different dimensions
By default, reshape() reshapes the array along the 0th dimension (row). This behavior can be changed via the order='C' parameter (default value is 'C'). See documentation for more information.
a1.reshape(3, 4) # reshapes or 'fills in' row by row
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
a1.reshape(3, 4, order='C') # same as above because default order='C'
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
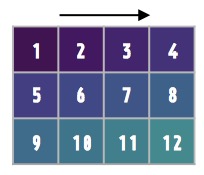
We can reshape along the 1st dimension (column) by specifying order='F'. For those familiar with MATLAB, MATLAB uses order='F'.
a1.reshape(3, 4, order='F') # reshapes of 'fills in' column by column
array([[ 1, 4, 7, 10],
[ 2, 5, 8, 11],
[ 3, 6, 9, 12]])
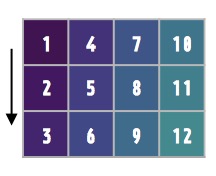
Test: a1 is a 1D array—it has only 1 dimension, even though you might think it’s dimension should be 1_12 (1 row by 12 columns). To convert to a 1_12 array, use reshape.
print(a1)[ 1 2 3 4 5 6 7 8 9 10 11 12]
print(a1.shape) # just (12,)(12,)
a1_1_by_12 = a1.reshape(1, -1)
print(a1_1_by_12) # note the double square brackets![[ 1 2 3 4 5 6 7 8 9 10 11 12]]
print(a1_1_by_12.shape) # 1_12 array(1, 12)
Flatten/ravel to 1D arrays with ravel()
The ravel() method lets you convert multi-dimensional arrays to 1D arrays (see docs here). Our 2D array (3_4) will be flattened or raveled such that they become a 1D array with 12 elements.
If you don’t specify any parameters, ravel() will flatten/ravel our 2D array along the rows (0th dimension/axis). That is, row 0 [1, 2, 3, 4] + row 1 [5, 6, 7, 8] + row 2 [9, 10, 11, 12].
If you want to flatten/ravel along the columns (1st dimension), use the order parameter.
print(a1_2d) # 3_4[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
print(a1_2d.ravel()) # ravel by row (default order='C')[ 1 2 3 4 5 6 7 8 9 10 11 12]
print(a1_2d.ravel(order='F')) # ravel by column[ 1 5 9 2 6 10 3 7 11 4 8 12]
Concatenate/stack arrays with np.stack() and np.hstack()
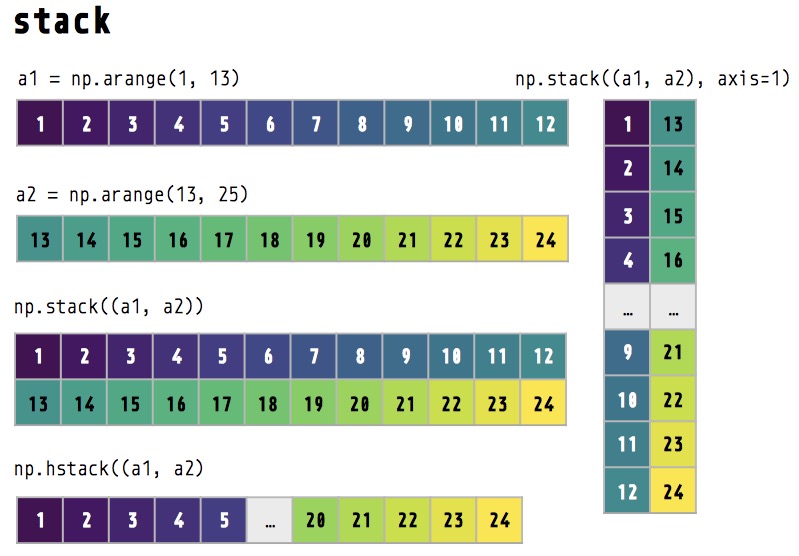
Create two 1D arrays
a1 = np.arange(1, 13)
print(a1)[ 1 2 3 4 5 6 7 8 9 10 11 12]
a2 = np.arange(13, 25)
print(a2)[13 14 15 16 17 18 19 20 21 22 23 24]
Use np.stack() to concatenate/stack arrays
By default, np.stack() stacks arrays along the 0th dimension (rows) (parameter axis=0). See docs for more info.
stack0 = np.stack((a1, a1, a2, a2)) # default stack along 0th dimension/axis (row)
print(stack0.shape)(4, 12)
print(stack0)[[ 1 2 3 4 5 6 7 8 9 10 11 12] [ 1 2 3 4 5 6 7 8 9 10 11 12] [13 14 15 16 17 18 19 20 21 22 23 24] [13 14 15 16 17 18 19 20 21 22 23 24]]
Stack along the 1st dimension (axis=1)
stack1 = np.stack((a1, a1, a2, a2), axis=1)
print(stack1.shape)(12, 4)
print(stack1)[[ 1 1 13 13] [ 2 2 14 14] [ 3 3 15 15] [ 4 4 16 16] [ 5 5 17 17] [ 6 6 18 18] [ 7 7 19 19] [ 8 8 20 20] [ 9 9 21 21] [10 10 22 22] [11 11 23 23] [12 12 24 24]]
Concatenate as a long 1D array with np.hstack() (stack horizontally)
stack_long = np.hstack((a1, a2))
print(stack_long.shape)(24,)
print(stack_long)[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
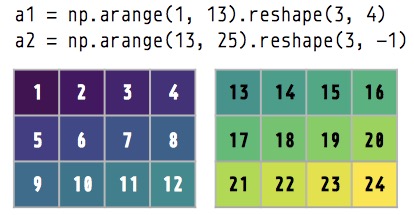
Create multi-dimensional array (3D)
Create two different 3 by 4 arrays.
a1 = np.arange(1, 13).reshape(3, -1) # 3_4
print(a1)[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
a2 = np.arange(13, 25).reshape(3, -1) # 3_4
print(a2)[[13 14 15 16] [17 18 19 20] [21 22 23 24]]
Create a 3D array by stacking the arrays along different axes/dimensions
a3_0 = np.stack((a1, a2)) # default axis=0 (dimension 0)
a3_1 = np.stack((a1, a2), axis=1) # dimension 1
a3_2 = np.stack((a1, a2), axis=2) # dimension 2Inspect the 3D arrays. Note the three 3D arrays have different shapes.
print(a3_0.ndim) # number of dimension3
print(a3_0.size) # number of elements in array24
print(a3_0.shape) # 2_3_4(2, 3, 4)
print(a3_0)[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_1.shape) # 3_2_4(3, 2, 4)
print(a3_1)[[[ 1 2 3 4] [13 14 15 16]] [[ 5 6 7 8] [17 18 19 20]] [[ 9 10 11 12] [21 22 23 24]]]
print(a3_2.shape) # 3_4_2(3, 4, 2)
print(a3_2)[[[ 1 13] [ 2 14] [ 3 15] [ 4 16]] [[ 5 17] [ 6 18] [ 7 19] [ 8 20]] [[ 9 21] [10 22] [11 23] [12 24]]]
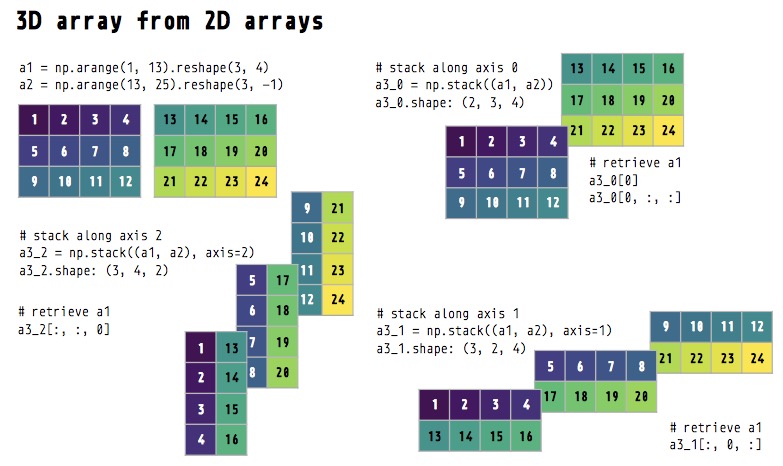
Because the three 3D arrays have been created by stacking two arrays along different dimensions, if we want to retrieve the original two arrays from these 3D arrays, we’ll have to subset along the correct dimension/axis.
Reminder of what a1 array looks like before we retrieve it from our 3D arrays.
print(a1) # reminder of what a1 is[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
Retrieve a1 from 0th dimension. Note the
print(a3_0.shape)(2, 3, 4)
print(a3_0)[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_0[0, :, :]) # idx 0 along 0th dimension[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
a3_0[0] # same as above
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
Retrieve a1 from 1st dimension
print(a3_1.shape)(3, 2, 4)
print(a3_1)[[[ 1 2 3 4] [13 14 15 16]] [[ 5 6 7 8] [17 18 19 20]] [[ 9 10 11 12] [21 22 23 24]]]
print(a3_1[:, 0, :]) # idx 0 along 1st dimension[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
Retrieve a1 from 2nd dimension
print(a3_2.shape)(3, 4, 2)
print(a3_2)[[[ 1 13] [ 2 14] [ 3 15] [ 4 16]] [[ 5 17] [ 6 18] [ 7 19] [ 8 20]] [[ 9 21] [10 22] [11 23] [12 24]]]
print(a3_2[:, :, 0]) # idx 0 along 2nd dimension[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]]
Flatten multidimensional arrays
We can also flatten multi-dimensional arrays with ravel().
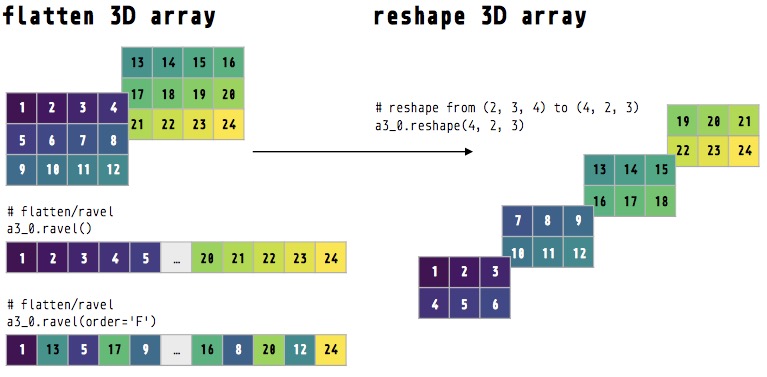
Ravel row by row (default order='C') to 1D array
print(a3_0)[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_0.ravel())[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
Ravel column by column (order='F') to 1D array
print(a3_0)[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_0.ravel(order='F'))[ 1 13 5 17 9 21 2 14 6 18 10 22 3 15 7 19 11 23 4 16 8 20 12 24]
Reshape multidimensional arrays
We can also use reshape() to reshape multi-dimensional arrays.
Reshape row by row (default order='C') to 2D array
print(a3_0) # 2_3_4[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_0.reshape(4, -1)) # reshape to 4_6 (row by row)[[ 1 2 3 4 5 6] [ 7 8 9 10 11 12] [13 14 15 16 17 18] [19 20 21 22 23 24]]
Reshape row by row (order=F) to 2D array
print(a3_0.reshape(4, -1, order='F')) # reshape to 4_6 (column by column)[[ 1 9 6 3 11 8] [13 21 18 15 23 20] [ 5 2 10 7 4 12] [17 14 22 19 16 24]]
Reshape row by row (default order='C') to 3D array
print(a3_0) # 2_3_4[[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[13 14 15 16] [17 18 19 20] [21 22 23 24]]]
print(a3_0.reshape(4, 2, 3)) # reshape to 4_2_3 (row by row)[[[ 1 2 3] [ 4 5 6]] [[ 7 8 9] [10 11 12]] [[13 14 15] [16 17 18]] [[19 20 21] [22 23 24]]]